Measuring the Size of the Earth

- with a strings, ruler, rock, sticks and horizon

This page provides the geometric proofs used in the video To Measure the Size of the Earth.

Homepage
Video's, How To's, etc.

video

Distance to the Horizon

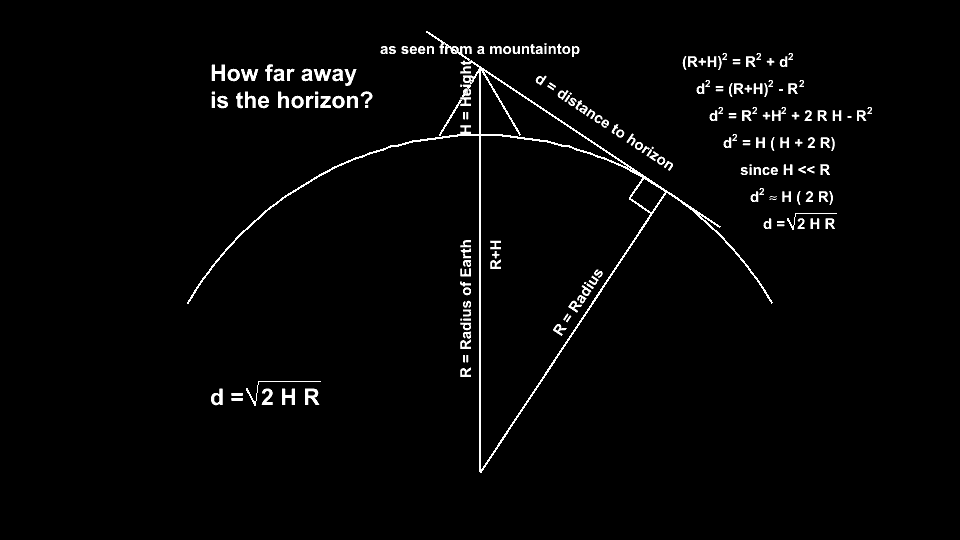
There are a few essential concepts and one approximation which we need.

  • When you are on a mountain, you are a distance of R + H from the center of the Earth.
    R + H = (Radius of Earth) + (Height of Mountain)
  • The horizon, at sea-level, is a distance R from the center of the Earth.
    R = (Radius of Earth)
  • Your line of sight to the horizon is tangential to the surface of the Earth, and so perpendicular to a line from the center of the Earth to a point on your horizon.
So here is the proof
  • (R+H)2 = R2 + d2
  • d2 = (R+H)2 - R2
  • d2 = R2 + H2 + 2 R H - R2
  • d2 = H ( H + 2 R)
  • d2 = H ( 2 R)
  • d = √(2 H R)
  • Pythagorian Theorem
  • solve for d
  • expand
  • R2 and -R2 cancel
  • H is much, much smaller then 2 R (see below)
  • take the square-root of both side.
Dropping the H because it is much smaller then 2 R is very reasonable. But if you want to keep it, then d = √(2 H R + H2)

Radius of the Earth

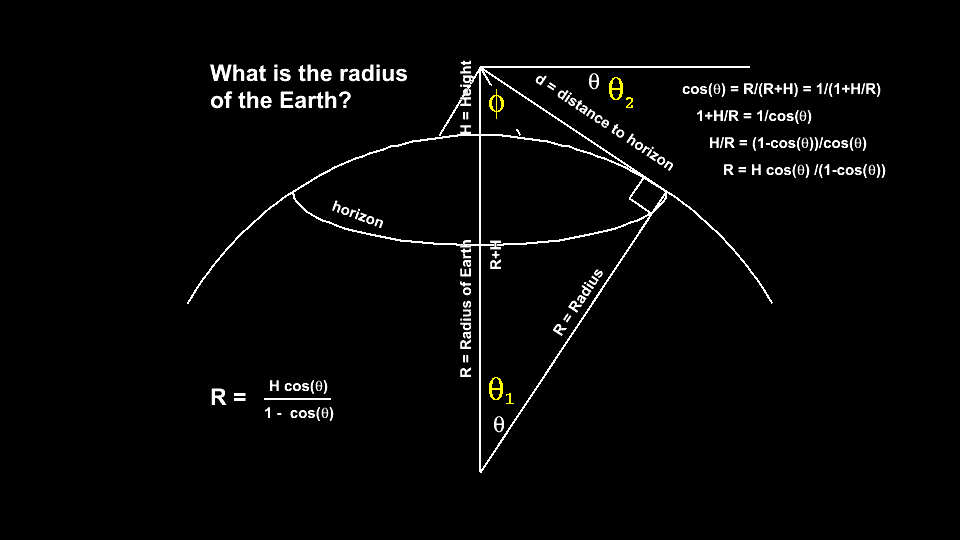
First we need to show that the angle of the arc and the dip angle are the same. The angle of the arc is marked in yellow as θ1 and the dip angle is θ2

Proof
  • θ1 + φ = π/2 = 90o
  • θ2 + φ = π/2 = 90o
  • therefore θ1 = θ2 = θ
  • sightline is horizontal, line to Earth-center is vertical
  • angles in a triangle add to π and other angle is π/2
  • -
Now to solve for the radius of the Earth
  • cos(θ) = adjacent/hypotenuse = R/(R+H)
  • cos(θ) = 1/(1+H/R)
  • 1+H/R = 1/cos(θ)
  • H/R = 1/cos(θ) - 1 = 1/cos(θ) - cos(θ)/cos(θ)
  • H/R = (1 - cos(θ))/cos(θ)
  • R = H cos(θ)/(1-cos(θ))
  • defination of cos
  • divide everthing on the right by R
  • rearrange (I am solving for R)
  • subtract 1 from boths sides
  • collect the common cos(θ)
  • solve for R

Dip Angle - Ideal

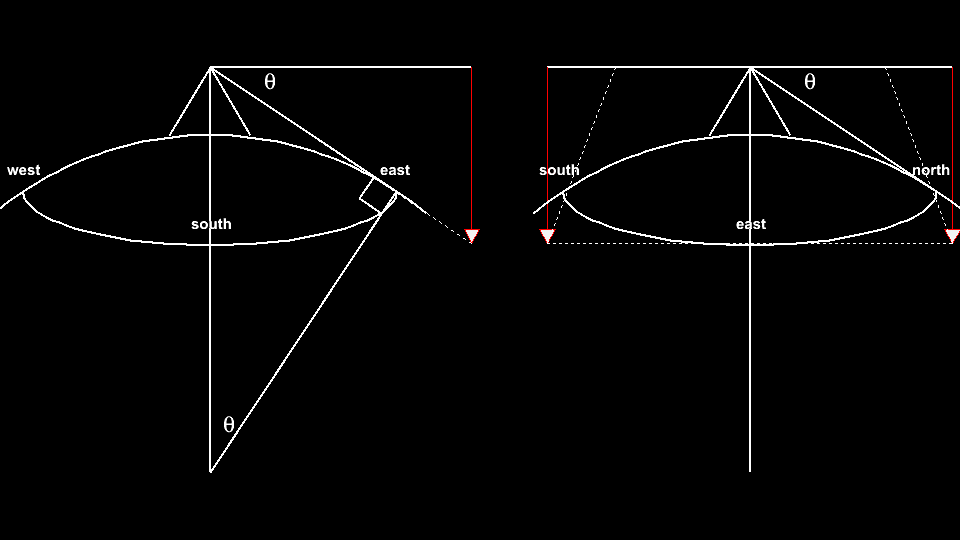
So the difficulty is to measure the dip angle: θ, that is the angle you have to look down to see the horizon. There are undoubtedly many ways of doing this, but I wanted to confine my appartuse to strings and rulers.

So the method I chose was to imagine a horizontal plane. I can tip it around the north-south axis until it touchs the eastern horizon. To the north and south the angle is still θ.

Experimentally I can create this plane with two sticks and a point on the horizon. To the east, this plane touches the horizon. To the north and south it rises by θ.

This plane, of course, does not have to be orinted along the north-south axis, and touching to the east. If you are high up and have 180o of ocean horizen, you can then do the measurement.

I, however, did not have 180o of clear ocean view.

Dip Angle - Real measurement

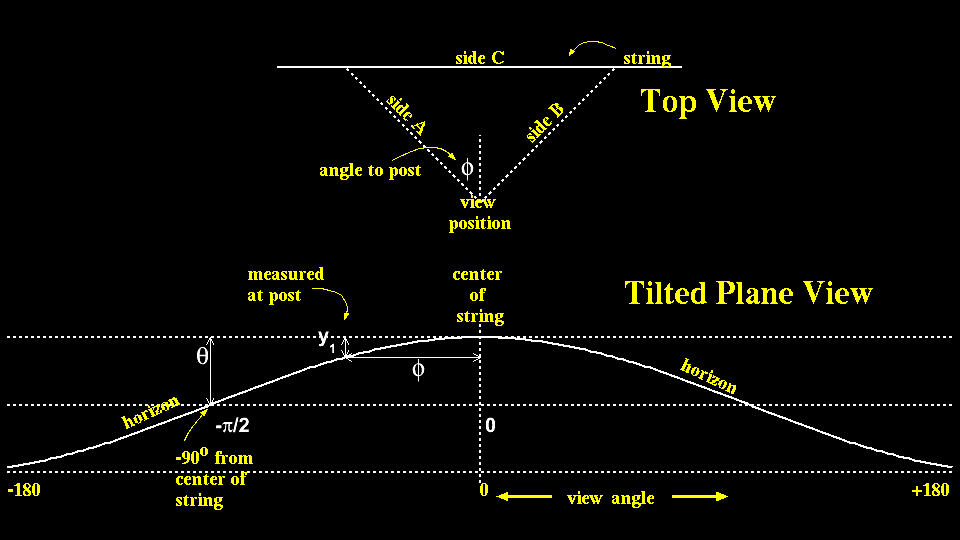So I can take the dip angle as measured at the post (y1) and by knowing the angle from the center of the string to the post (φ) I can calculate the dip angle at 90o (θ):

  • y1 = (1 - cos φ)*θ
  • θ = y1 / (1 - cos φ)
Also the angle φ is calculated from the sides of the trangle instead of directly, since I did not have a protractor. But it is straightforward with the Law of Cosines
  • c2 = a2 + b2 - a b cos(2 φ)
or:
  • φ = cos-1(a2 + b2 - c2)/( 4 a b)

Putting in the Numbers

  1. Calculate φ
    • a = 350 cm
    • b = 360 cm
    • c = 395 cm
    • φ = 0.590 rad = 33.8o
  2. Calculate y1, y2 and yavg
    • dip1 = 1.5 mm = 0.15 cm
    • y1 = 0.15 cm / 350 cm = 0.000429 rad = 0.0246o
    • dip2 = 1.5 mm = 0.15 cm
    • y2 = 0.15 cm / 360 cm = 0.000417 rad = 0.0239o
    • yavg = 0.000423 rad = 0.0242o
  3. Calculate dip angle θ
    • θ = = yavg / (1 - cos φ)
    • θ = 0.00250 rad = 0.143o
  4. Radius of the Earth R
    • R = H cos(θ)/(1-cos(θ))
    • H = 24.22 m
    • Rthis measurement = 7,740,000 m = 7,700 km
    • Rstandard = 6,371 km